



| Advanced Java Services | Binäre Suchbäume (Binary Search Tree, BST) |




|
Ein binärer Baum heißt binärer Suchbaum (BST), wenn er die folgenden Bedingungen erfüllt.
Die folgenden beiden Suchbäume sind vollständig ausgeglichen.
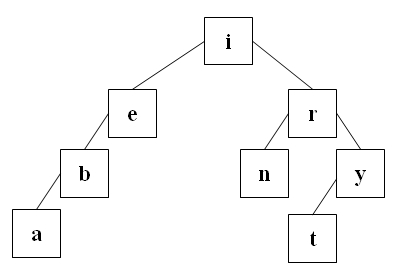
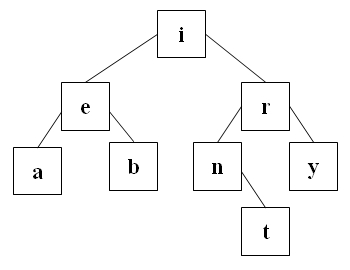
Der folgende Suchbaum ist zu einer einfach verketteten Liste entartet.
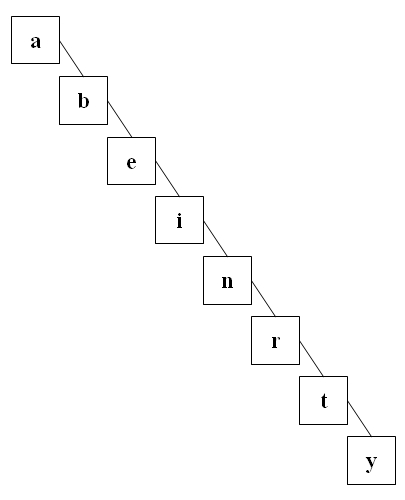
Die Bedeutung binärer Suchbäume liegt darin, daß sich Daten in den so geordneten Bäumen extrem schnell finden lassen, falls der Baum ausgeglichen oder fast ausgeglichen ist. In der Praxis enthält einen Knoten neben den beiden Zeigern noch mindestens zwei weitere Daten, einmal den Schlüssel, nach dem die Daten geordnet sind und zum anderen den eigentlichen Datenteil. Das sieht prinzipiell folgendermaßen aus.
struct data
{
//...
};
struct node
{
int key;
struct data value;
struct node* left;
struct node* right;
}
Die Daten sind also nach dem key geordnet. In unseren Beispielen bleiben wir jedoch bei der bisher verwendeten Struktur, setzen also für Schlüssel und Daten nur eine int-Variable ein.
Der Vorteil eines geordneten Baumes ist, daß Elemente sehr schnell über binäres Suchen gefunden werden können. Wir bauen den Baum von Anfang an geordnet auf und verwenden dabei den von Niklas Wirth beschriebenen Algorithmus.
Die wesentliche Arbeit wird von der rekursiven Funktion searchAndInsert erledigt. Wie die Funktion arbeitet, wird an dem folgenden Beispiel deutlich.
void searchAndInsert(node** nod, int ch)
{
if (*nod == NULL)
{
*nod = createNode(ch);
printf("new node %c ", ch);
}
else
{
if( ch < (*nod)->ch)
{
printf("left %c ", ch);
searchAndInsert( &((*nod)->left), ch);
}
else if ( ch > (*nod)->ch)
{
printf("right %c ", ch);
searchAndInsert(&((*nod)->right), ch);
}
else
{
printf("duplicate %c ", ch); // already in tree
}
}
}
Nun muß lediglich noch die obige Funktion für jedes Element des Arrays aufgerufen werden.
/*
* Ruft zu jedem Arrayelemenmt searchAndInsert auf
*/
node* build_BST_FromArray(node* node, int* arr, int size)
{
if (arr == null || size == 0) return null;
node* root = node;
for(int i=0; i<size; i++)
{
searchAndInsert(&root, arr[i]);
//printf("done %c %d\n", arr[i], i);
}
return root;
}
Wir verwenden das folgende Array:
int arr[] = {'b', 'i', 'n', 'a', 'r', 'y', 't', 'r', 'e', 'e'};
Damit ergibt sich folgender Baum:
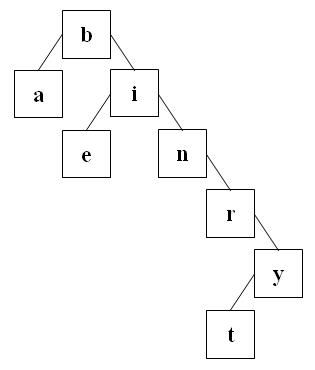
Da der Baum eine minimale Tiefe von 2 und eine maximale Tiefe von 6 hat ist er leider nicht ausgeglichen
Wir wählen eine andere Reihenfolge im Array, indem wir mit einem Buchstaben beginnen der ungefähr in der Mitte liegt.
int arr[] = {'n', 'i', 'b', 'a', 'r', 'y', 't', 'r', 'e', 'e'};
Jetzt ergibt sich der folgende Baum:
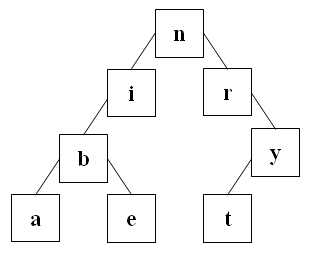
Dieser Baum ist vollständig ausgeglichen.
Wir wollen das Löschen natürlich so gestalten, daß der dabei entstehende Baum wieder ein Suchbaum ist. Ist der zu löschende Knoten ein Blatt, so ist das Löschen einfach. Auch wenn der zu löschende Knoten nur einen Nachfolger hat ist das Löschen offensichtlich. Um den schwierigen Fall zu verdeutlichen geben wir uns folgenden Suchbaum vor:
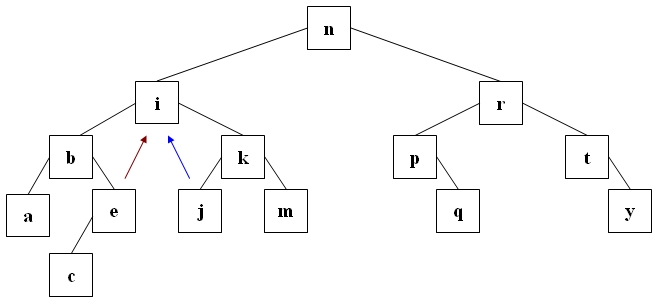
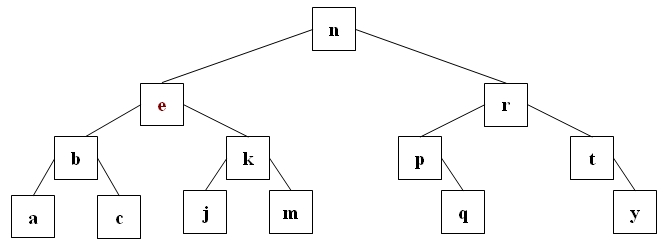
Wollen wir hier i löschen, so muß dieses Element entweder durch das größte Element des linken Teilbaum ersetzt werden (e)
oder durch das kleinste Element des rechten Teilbaum ersetzt werden (j).
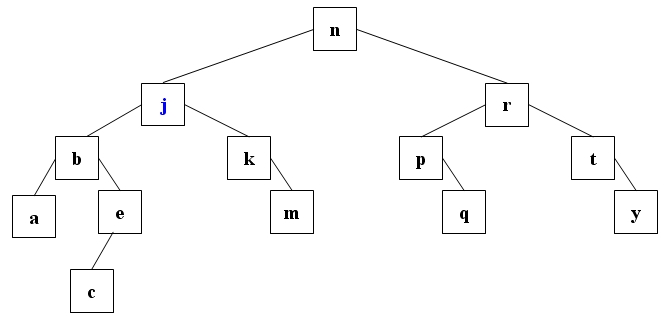
Beide Varianten sind gleichwertig. Die meisten Implementierungen arbeiten mit der ersten Variante. Der hier vorgestellte Algorithmus stammt von Niklaus Wirth, dessen Pascalcode nach C übersetzt wurde.
Der Code besteht aus zwei Teilen. Die erste Funktion arbeitet solange rekursiv bis man den Knoten mit dem übergebenen Daten gefunden hat (oder es keinen gibt). Anschließend wird der gefundene Knoten untersucht und die oben besprochenen drei Fälle unterschieden. Die ersten beiden Fälle sind mit jeweils einem Statement zu erledigen, für den schwierigen dritten Fall, daß ein Knoten zwei Nachfolger hat wird in die Hilfsfunktion del verzweigt.
/*
* Funktion für des Löschen in einem BST
*/
void delete(node** pNode, int ch)
{
node* q = NULL;
if (pNode == NULL)
{
printf("%c nicht im baum\n", ch);
}
else if( ch < (*pNode)->ch)
{
delete(&((*pNode)->left), ch);
}
else if (ch > (*pNode)->ch)
{
delete(&((*pNode)->right), ch);
}
else // Löschen
{
q = *pNode;
if (q->right == NULL)
{
q = q->left; // lifte den linken Teilbaum
}
else if (q->left == NULL)
{
q = q->right; // lifte den rechten Teilbaum
}
else
{
printf("der schwierige fall %c %c\n", q->ch, q->left->ch); // i, b
del(&q, &(q->left));
free(q);
}
}
}
Die Hilfsfunktion
/*
* Hilfsfunktion für des Löschen in einem BST
*/
void del(node** q, node** qleft)
{
if ((*qleft)->right != NULL)
{
del(q, &((*qleft)->right));
// deswegen brauch man zwei parameter !
}
else
{
(*q)->ch = (*qleft)->ch; // deswegen braucht man **q
*q = *qleft;
*qleft = (*qleft)->left; // deswegen braucht man **qleft
}
}
Robert Sedgewick: Algorithmen. Addison-Wesley, 1992, Kapitel 4 und 5
Niklaus Wirth: Algorithmen und Datenstrukturen. Teubner, 1983, Kapitel 4.4 Baumstrukturen
GeeksforGeeks, www.geeksforgeeks.org/level-order-tree-traversal/, 20.08.2013.
GeeksforGeeks, www.geeksforgeeks.org/write-a-c-program-to-calculate-size-of-a-tree/, 20.08.2013.
Nick Parlante, Binary Trees, cslibrary.stanford.edu/110/BinaryTrees.html, 20.08.2013.
|
|





|