



| Advanced Java Services | Binäre Bäume |




|
Ein binärer Baum ist eine Datenstruktur, bei der - im Gegensatz zu einer einfach verketteten Liste - ein Element zwei Nachfolger hat. Die Elemente nennt man Knoten. Sind beide Nachfolger eines Knotens NULL so spricht man von einem Blatt oder Blattknoten. Der Knoten der keinen Vorgänger hat wird Wurzel oder Root genannt. Die graphische Darstellung eines Baumes beginnt immer mit der Wurzel. In der folgenden Abbildung ist b die Wurzel des Baumes, n und a haben nur einen linken Nachfolger und r nur einen rechten Nachfolger. y, r und die beiden e sind Blätter. Der Baum hat maximal 6 Stufen und minimal 3 Stufen. Die sechste Stufe ist nur mit y besetzt, in der dritten Stufe findet man n, t, e, e .
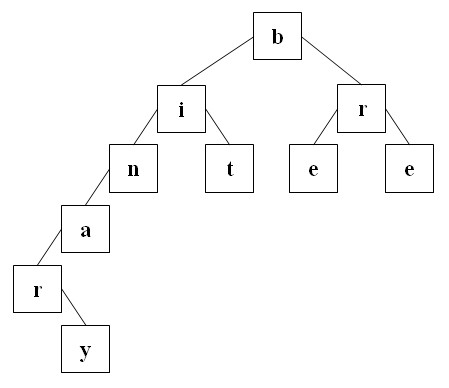
Ein binärer Baum heißt vollständig ausgeglichen, wenn sich minimale und maximale Stufenhöhe höchstens um eins unterscheiden.
Der folgende Baum ist vollständig ausgeglichen.
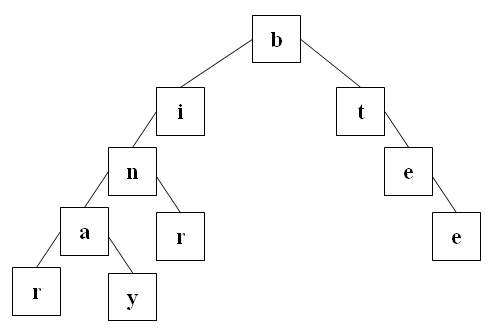
Ein binärer Baum heißt geordnet, wenn die Daten eine Ordnungsrelation erfüllen, also vergleichbar sind und für jeden Knoten gilt, daß der linke Nachfolger kleiner (oder kleiner gleich) dem rechten Nachfolger ist (oder umgekehrt).
Der folgende Baum ist durch "<=" geordnet und nicht ausgeglichen.
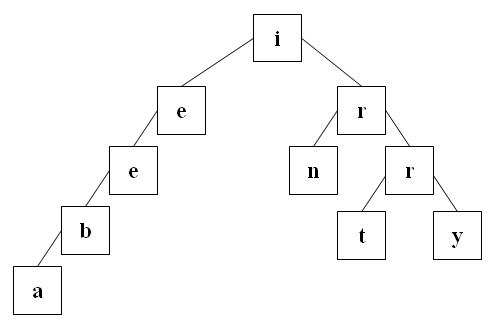
Ein binärer Baum heißt binärer Suchbaum (BST), wenn er die folgenden Bedingungen erfüllt.
Der folgende Baum ist ein durch "<" geordneter und ausgeglichener BST.
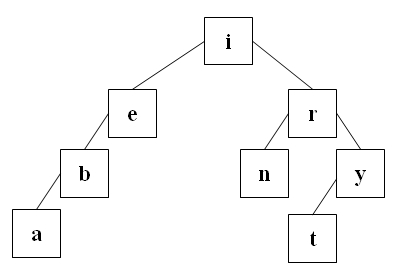
Binäre Suchbäume werden im nächsten Kapitel behandelt.
Man unterscheidet gewöhnlich vier verschiedene Arten, einen Baum zu durchschreiten:
Man sieht, daß die ersten drei Traversierungen rekursiv definiert sind.
Als Beispiel traversieren wir den Baum aus der ersten Abbildung nach allen vier Varianten:

|
|
Wie zu erwarten realisieren wir den Knoten durch ein struct.
struct node
{
int ch;
struct node *left;
struct node *right;
};
typedef struct node node;
Im Datenteil wählen wir den Typ int, so können wir Zeichen und Zahlen darstellen. Alle Beispiele und Operationen lassen sich aber auch mit komplexen Datentypen realisieren.
Die Funktion holt Speicher für einen Knoten, initialisiert den Datenteil und setzt die beiden Zeiger auf NULL. Zurückggeben wird ein Zeiger auf den Knoten oder Null, falls kein Speicher angefordert werden konnte.
node* createNode(int ch)
{
node *nod = malloc(sizeof(node));
if (nod != NULL)
{
nod->ch = ch;
nod->left = NULL;
nod->right = NULL;
}
return nod;
}
Hängt an nod links (bzw. rechts) einen neuen Knoten an. Falls NULL übergebn wird oder kein Speicher angefordert werden konnte wird NULL zurückgegeben, ansonsten der neue Knoten.
node* appendLeftNode(node* nod, int ch)
{
if (nod != NULL)
{
node *leftnode = malloc(sizeof(node));
if (leftnode != null)
{
leftnode->ch = ch;
leftnode->left = NULL;
leftnode->right = NULL;
nod->left = leftnode;
}
return leftnode;
}
return nod;
}
node* appendRightNode(node* nod, int ch)
{
if (nod != NULL)
{
node* rightnode = malloc(sizeof(node));
if (rightnode != null)
{
rightnode->ch = ch;
rightnode->left = NULL;
rightnode->right = NULL;
nod->right = rightnode;
}
return rightnode;
}
return nod;
}
Mit Hilfe dieser beiden Funktionen können wir den oben abgebildeten Baum leicht aufbauen.
int main(void)
{
node* root = createNode('b');
printf("root = %c\n", root->ch); // b
node* node_i = appendLeftNode(root, 'i');
node* node_n = appendLeftNode(node_i, 'n');
node* node_t = appendRightNode(node_i, 't');
node* node_a = appendLeftNode(node_n, 'a');
node* node_r1 = appendLeftNode(node_a, 'r');
node* node_y = appendRightNode(node_r1, 'y');
node* node_r2 = appendRightNode(root, 'r');
node* node_e1 = appendLeftNode(node_r2, 'e');
node* node_e2 = appendRightNode(node_r2, 'e');
return EXIT_SUCCESS;
}
Zum Traversieren codieren wir die weiter oben angeführten rekursiven Algorithmen. Preorder, Inorder und Postorder verwenden im Grunde denselben Algorithmus und erledigen ihre Aufgabe nur an unterschiedlichen Stellen, wie das folgende Schem zeigt.
void traverse(node* root)
{
if (root == null) return;
// preorder task
traverse(root->left);
// inorder task
traverse(root->right);
// postorder task
}
Wenn wir den Baum ausgeben wollen brauchen wir lediglich printf() an den entsprechenden Stellen einfügen.
Preordertraversierung
void printTreeInPreorder(node* root)
{
if (root == null) return;
printf("%c ", root->ch);
printTreeInPreorder(root->left);
printTreeInPreorder(root->right);
}
Inordertraversierung
void printTreeInInorder(node* root)
{
if (root == null) return;
printTreeInInorder(root->left);
printf("%c ", root->ch);
printTreeInInorder(root->right);
}
Postordertraversierung
void printTreeInPostorder(node* root)
{
if (root == null) return;
printTreeInPostorder(root->left);
printTreeInPostorder(root->right);
printf("%c ", root->ch);
}
Wir verwenden den gleichen Algorithmus um die Anzahl der Knoten zu ermitteln. Als Zähler wird eine statische Variable verwendet, die bekanntlich nur einmal initialisiert wird. In diesem Fall ist es egal, wo der Zähler inkrementiert wird.
int nodeCount(node* root)
{
static int count = 0;
if (root == NULL) return 0;
count++;
nodeCount(root->left);
nodeCount(root->right);
return count;
}
Die folgende Variante kommt ohne statische Variable aus.
int nodeCount(node* root)
{
if (root==NULL) return 0;
return nodeCount(root->left) + 1 + nodeCount(root->right) ;
}
Eine weitere Abwandlung dieses Algorithmus' liefert uns die maximale Tiefe eines Baumes.
int maxTreeDepth(node* nod)
{
//if (nod == NULL) return -1; // Erste Stufe erhält Index 0
if (nod == NULL) return 0; // Erste Stufe erhält Index 1
int lheight = maxTreeDepth(nod->left);
int rheight = maxTreeDepth(nod->right);
return (lheight > rheight) ? lheight+1 : rheight+1;
}
Leider läßt sich der obige Algorithmus nicht verwenden um die minimale Tiefe eines Baumes zu ermitteln. Hier gehen wir einen andseren Weg. Einer Hilfsfunktion übergibt man eine obere Grenze für das Minimum, etwa die Anzahl der Knoten, als Zeiger. Die Hilfsfunktion verbessert dann erkursiv diesen Startwert bis das Minimum erreicht ist.
Die Hilfsfunktion seekMin
/*
* Hilfsfunktion zur Ermittlung der kürzesten Pfadlänge
*/
void seekMin(node* node, int* min, int pathLen)
{
if (node==NULL) return ;
pathLen++;
if (node->left == NULL && node->right == NULL)
{
if ( pathLen != 0 && pathLen < *min)
{
*min = pathLen;
}
}
else
{
seekMin(node->left, min, pathLen);
seekMin(node->right, min, pathLen);
}
}
Die Funktion minTreeDepth stützt sich auf die obige Funktion
/*
* Ermittelt die minimale Pfadlänge mit Hilfe der Funktion seekMin
*/
int minTreeDepth(node* node)
{
int min = nodeCount(node);
seekMin(node, &min, 0);
return min;
}
Eine erneute Variation des Standardalgorithmus' ermöglicht die Ausgabe aller Knoten einer Stufe.
void printTreeLevel(node* root, int level)
{
if(root == NULL || level <= 0) return;
if (level == 1)
printf("%c ", root->ch);
else
{
printTreeLevel(root->left, level - 1);
printTreeLevel(root->right, level - 1);
}
}
Da wir die Stufentiefe ermitteln können und alle Knoten einer Stufe ausgeben können ist die folgende Funktion offensichtlich.
/*
* Verwendet printTreeLevel und maxTreeDepth
*/
void printTreeInLevelorder(node* root)
{
int size = maxTreeDepth(root) +1;
for(int i=1; i < size; i++)
{
printTreeLevel(root, i);
printf(" ");
}
}
Der Standardalgorithmus hilft uns auch in diesem Fall. Es gibt allerdings nur eine richtige Reihenfolge und diese ist Postorder weil root immer am Schluß besucht werden muß. Einfügen von printf zeigt das.
/*
* Löschen des ganzen Baumes
*/
void deleteTree (node *root )
{
if ( root == NULL ) return;
deleteTree(root->left);
deleteTree(root->right);
//printf("-%c ", root->ch);
free(root);
}
Wir verwenden den von Niklaus Wirth beschriebenen rekursiven Algorithmus um einen Baum ausgeglichen aufzubauen.
/*
* Baut einen ausgeglichenen binären Baum mit Buchstaben
* Dazu wird ein Array von Buchstaben übergeben
* Um den jeweils nächsten Buchstaben zu verwenden wird die
* Arrayposition in einer statischen Variablen gespeichert.
*/
node* buildTreeFromArray(char* arr, int size)
{
static int pos = 0;
if (arr == null || size == 0)
return null;
int sizeleft = size / 2, sizeright = size - sizeleft - 1;
node* newnode = createNode(arr[pos++]);
// beim ersten mal ist das root
if (newnode != null)
{
newnode->left = buildTreeFromArray(arr, sizeleft);
newnode->right = buildTreeFromArray(arr, sizeright);
}
return newnode;
}
Wir übergeben das folgende Array
char arr[] = {'t', 'h', 'i', 's', 'i', 's', 'a', 'b', 'i', 'n', 'a', 'r', 'y', 't', 'r', 'e', 'e'};
und erhalten damit diesen Baum:
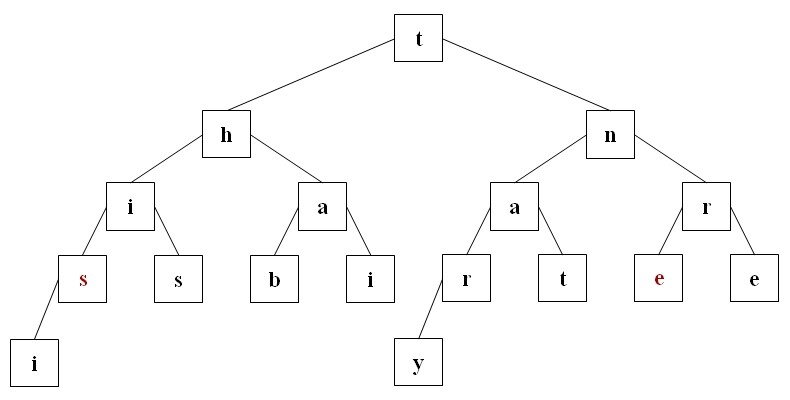
|
|
Mit etwas Mühe kann man die Anordnung des Baumes aus der Preorder-Reihenfolge eindeutig erschließen. Ebenso geht es mit Inorder und Postorder.Da die Stufen eins bis vier voll besetzt sind kann man die Abfolge auch aus der Levelorder-Reihenfolge schließen, lediglich bei der sechsten Stufe ist nicht klar, wo die beiden Knoten hängen. Man kann jedoch auch alle Pfade von der Spitze zu den Blättern einzeln ablaufen. Nick Parlante hat diesen Algorithmus vorgestellt, den wir hier in einer kleinen Variante zeigen.
Um die Idee nachvollziehn zu können gehen wir von der Preorderanordnung aus und fügen nach jedem Blatt einen Zeilenvorschub ein. Überdies schreiben wir Buchstaben auf ein und demselben Level in einer Spalte untereinander
t h i s i s a b i n a r y t r e e
Wenn es nun gelingt die Pfadanfänge der vorigen Zeile von der ersten Zeile an zu übernehmen, dann haben wir alle Pfade ausgehend von Root aus gefunden.
t h i s i " " " s " " a b " " " i " n a r y " " " t " " r e " " " e
Am einfachsten ist es die Elemente in ein Array zu schreiben, sich die Position zu merken und dann die alten Werte zu überschreiben. Das Array muß dabei mindestens so groß sein, wie der Baum Stufen hat.
Zum Ausgeben des Arrays wird eine kleine Hilfsfunktion bereitgestellt
void printArr(int arr[], int len)
{
for (int i=0; i <len; i++)
{
printf("%c ", arr[i]);
}
printf("\n");
}
Die Hauptarbeit erledigt die folgende Funktion
void printPaths(node* node, int path[], int pathLen)
{
if (node==NULL) return;
// append this node to the path array
path[pathLen] = node->ch;
pathLen++;
// it's a leaf, so print the path that led to here
if (node->left==NULL && node->right==NULL)
{
printArr(path, pathLen);
}
else
{
// otherwise try both subtrees
printPaths(node->left, path, pathLen);
printPaths(node->right, path, pathLen);
}
}
Nun müssen wir nur noch ein Array anlegen und die obige Funktion aufrufen
void printAllPaths(struct node* node)
{
int len = maxTreeDepth(node);
int path[len];
printPaths(node, path, 0);
}
Die Ausgabe
t h i s i t h i s t h a b t h a i t n a r y t n a t t n r e t n r e
|
|





|