



-
Schreiben Sie eine rekursive Methode double fibo(int n) . fibo soll die n-te Fibonaccizahl berechnen. Da die Fibonaccizahlen sehr schnell sehr groß werden, soll für Argumente größer 92 die statische Konstante Double.POSITIVE_INFINITY der Klasse Double zurückgegeben werden. Der rekursive Algorithmus lautet
fibo(n) = fibo(n-1) + fibo(n-2)
Startwerte
fibo(0) = 0 , fibo(1) = 1 -
Schreiben Sie eine rekursive Methode double binko(int n, int v) . binko ermittelt den Binomialkoeffizienten zu n und v, also n über v. Dazu verwenden Sie die folgende Rekursionsformel
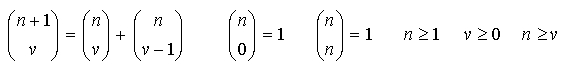
-
Schreiben Sie eine rekursive Methode int ggt(int a, int b) . ggT ermittelt den größten gemeinsamen Teiler der Zahlen a und b. Für eine rekursive Methode ziehen Sie die folgende von Euklid ( 325 - 265 BC ) entdeckte Eigenschaft heran:
Wenn a und b durch t teilbar sind, so auch a%b .
Legen Sie alle Methoden statisch an. Testen Sie ihre Methoden durch Aufrufe in main .




