Advanced   Java   Services

Rekursive Methoden

sind etwas für Tüftler, die Freude an logischen Knobeleien haben. Bei den Methoden haben wir bereits den Vorgang eines Unterprogrammaufrufs dargetellt. In dem dort gezeigten Fall ruft ein ein Unterprogramm ein anderes Unterprogramm auf. Ein Unterprogramm kann sich aber auch selbst aufrufen, wobei auch in diesem Fall jeder Aufruf durch einen eigenen Speicherblock realisiert wird. Methoden, die mit dieser Technik arbeiten, nenn man rekursiv. Rekursive Methoden sind meist ebenso elegant wie gefährlich. Es ist wichtig, sich das Ende der Rekursion genau zu überlegen. Ist der Algorithmus fehlerheft und findet die Rekursion kein Ende, gibt es mit Sicherheit einen Programmabsturz, da der Stack zur Speicherung der Rücksprungadressen ja zwangsläufig nur begrenzte Kapazität hat. Auch bei einem sauberen Algorithmus kann es zu Problemen kommen, wenn auf dem Stack vor dem Ende der Rekursion kein Platz mehr ist.

Die folgende Graphik zeigt das Prinzip. Bei jeder Rekursion gibt es einen Hinweg (blaue Aufrufpfeile) und einen Rückweg (schwarze Rücksprungpfeile)



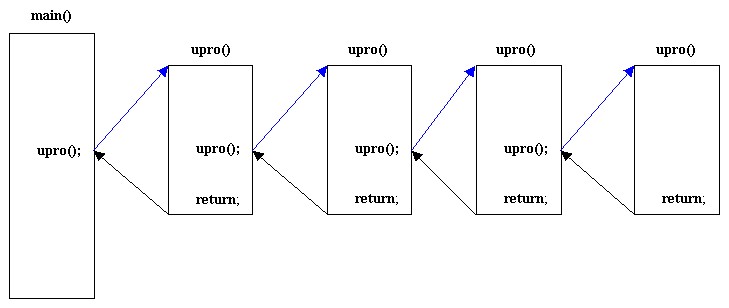
Das folgend Beispiel zeigt eine einfache Rekursion. Bei jedem Aufruf der Methode wird ein Zähler übergeben, den die Methode hochzählt. Erreicht der Zähler seinen Höchststand, dann endet die Rekursion. Die Werte des Zählers werden auf dem Hinweg und auf dem Rückweg jeweils ausgegeben.

public class Rekursion
{
   public static void main(String args[])
   {
      rekursiv(0) ;
   }

   public static void rekursiv(int a)
   {
      System.out.println("Hinweg "+ a );
      a++;
      if (a<5)
      {
         rekursiv(a);  // rekursiver Aufruf
      }
      System.out.println("Rueckweg " + a );
   }

} // end class

Das Programm macht die folgende Ausgabe

Hinweg 0
Hinweg 1
Hinweg 2
Hinweg 3
Hinweg 4
Rueckweg 5
Rueckweg 4
Rueckweg 3
Rueckweg 2
Rueckweg 1

Es ist wichtig, sich klar zu machen, daß alles, was vor dem rekursiven Aufruf steht, auf dem Hinweg passiert und alles, was nach dem rekursiven Aufruf steht, auf dem Rückweg stattfindet.

Die Berechnung der Fakultät ist das Standardbeispiel für rekursive Methoden. Sie wird für positive nichtnegative Zahlen (nur solche betrachten wir) folgendermaßen ermittelt:

7! = 1*2*3*4*5*6*7
2! = 1*2
1! = 1
0! = 1

Das läßt sich z.B. so codieren:

double fak(int n)
{
   double fak=1 ;

   for(int i=1; i<n; i++)
      fak = fak*(i+1) ;

   return fak;
}

Um daraus eine rekursive Methode zu machen brauchen wir einen rekursiven Algorithmus für die Fakultät. Der sieht so aus :

n! = (n-1)! * n

Der Anfang der Rekursion muß ebenfalls festgelegt werden. In diesem Fall kann er so aussehen.

0! = 1
1! = 1

Damit schreiben wir jetzt

double fak(int n)
{
   if(n<1)
      return 1;

   return fak(n-1)*n ;
}

Obige Zeilen ergeben für jedes negative Argument das Ergebnis 1, was mathematisch natürlich nicht korrekt ist. Es ist besser, einen Benutzer darauf hinzuweisen, daß er keine negativen Argumente verwenden soll. Dies kann durch das Auslösen einer Exception (siehe Exceptionhandling) erreicht werden. Wenn man dann noch den ternären Operator ?: verwendet, sieht unsere rekursive Methode wie folgt aus:

double fak(int n)
{
   if(n<0) throw new IllegalArgumentException("illegal argument : " + n);
   return n==0 ? 1 : fak(n-1)*n ;
}

Was manche Programmierer an rekursiven Methoden fasziniert ist ihre Kürze und ihre Eleganz.

Übung zu rekursiven Methoden